The Product of a Half-Turn and a Line Reflection is a Glide Reflection

(It is a line reflection if the center of the half-turn is on the mirror line.)

In this figure are two points A and B, the line AB = k, and the midpoint C of AB. Also shown are the lines m through C and n through A, both perpendicular to k.

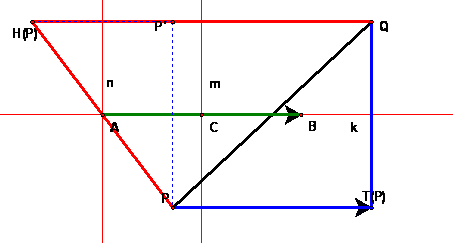
Let G denote the glide reflection G_AB with invariant line k and translation vector AB. For any point P, let Q = G(P).

We will show three ways to construct Q as a product of isometries. This will demonstrate that G is the product of a half-turn and a line reflection.

Let

T = T_AB, the translation that takes A to B and

K, M, N = reflections in lines k, m, n

H = halfturn H_A with center A

By definition, G = KT (Brown, p. 34). Let Q = G(P). We now study the figure to see 3 ways of constructing Q.

(1) Use the definition of glide reflection, which states G = KT.

Translate P to get T(P). Reflect T (P) in k to get Q = KT (P). By definition Q = G (P).

(2) Change the order of the translation and the glide to get Q = TK(P).

Reflect P in k to get P' = K(P). Then we claim Q = TP'). The reason this is true is that PP'QT (P) is a parallelogram (actually a rectangle). Since the sides PP' and T(P)Q are congruent and parallel, the quadrilateral is a parallelogram. Since PP'QT (P) is a parallelogram, the same translation T maps P to T(P) and also maps P' to Q. So Q = TK (P). (Since the angle at P is a right angle, the parallelogram is also a rectangle. If P is actually on line AB, a simple extra argument is needed for the special case.)

(3) Show Q = MH (P)

First, apply H to P to get H(P). Notice that H(P) = N(P') = NK(P). Then reflect in m to get MH (P) = MNK (P). Since MN = T (product of two parallel line reflections), then MH (P) = Q also.

Since P was any point, since MH (P) = G (P) for all P, then MH = G.

This shows that any glide reflection G is a product MH as explained above.

One more version of the same figure

The reasoning above did not use anything about P. While it is not necessary, it may be helpful to look at the same figure for a different P. Here is an example.

Proof of the Big Theorem about Half-turns and Line Reflections

Theorem: Let m be a line and let A be a point. Denote by A' the reflection of A in m.

Let k be the line through A perpendicular to m. Let n be the line through A parallel to m.

a) If A is on m, then R_m H_A = H_A R_m = R_k.

b) If A is not on m, then R_m H_A = G_AA', a glide reflection with invariant line k that maps A to A'.

c) If A is not on m, then H_A R_m = G_A'A, a glide reflection with invariant line k that maps A' to A.

Proof: The proof is essentially in the figure and discussion above, but starting with H and N and producing G rather than starting with G. Here is a short algebraic argument, without the figure and geometrical motivation.

Proof of (a)

If A is on m, then H_A = R_m R_k = R_k R_m.

Therefore, R_m H_A = R_m R_m R_k = R_k.

Likewise, R_k R_m = R_k R_m R_m = R_k.

Proof of (b)

The halfturn H_A = R_n R_k, so R_m H_A = R_m (R_n R_k) = (R_m R_n )R_k = T_AA' R_k .

We see that R_m R_n is a translation T, since m and n are parallel. Since T(A) = R_m (R_n(A)) = R_m (A) = A', T = T_AA'.

Proof of (c)

This is very similar to the proof of (b). This time we use H_A = R_k R_n. Then

H_A R_m = (R_k R_n)R_m = R_k (R_nR_m) = R_k T_A'A.

Again R_nR_m is a translation, but it is the inverse of the translation in (b), since the order of the reflections is reversed, so A' is mapped to A.

QED